Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Bruchrechnen macht dir auf den ersten Blick vielleicht etwas Angst, aber keine Sorge, es ist gar nicht so kompliziert, wie es zunächst erscheint. In diesem Artikel werde ich dir zeigen, wie Bruchrechnen im Alltag eine nützliche Fähigkeit sein kann und wie du Brüche addieren und subtrahieren kannst, ohne Kopfzerbrechen zu bekommen. Brüche addieren und subtrahieren – ganz leicht, wenn du die Grundprinzipien verstehst. Falls dir noch ein paar Grundlagen fehlen, lies doch erst einmal den Beitrag Einführung in Bruchrechnen.
Warum Bruchrechnen im Alltag wichtig ist
Bruchrechnen ist keine abstrakte Mathematik, die nur in der Schule benötigt wird. Tatsächlich begegnen uns Brüche ständig im Alltag. Ob beim Kochen, Einkaufen oder bei Finanzangelegenheiten, Bruchrechnen ist eine praktische Fertigkeit, die dir hilft, genaue Ergebnisse zu erzielen. In diesem Artikel zum Bruchrechnen im Alltag habe ich darüber schon ausführlich geschrieben.
Grundlagen des Bruchrechnens
Bevor wir uns mit dem Addieren und Subtrahieren von Brüchen befassen, lass uns die Grundlagen klären. Ein Bruch besteht aus zwei Teilen: dem Zähler und dem Nenner. Der Zähler gibt an, wie viele Teile wir haben, und der Nenner zeigt, in wie viele Teile die ganze Einheit aufgeteilt ist. Zum Beispiel ist in einem Bruch wie 1/4, “1” der Zähler und “4” der Nenner. Das bedeutet, wir haben 1 von 4 gleich großen Teilen.
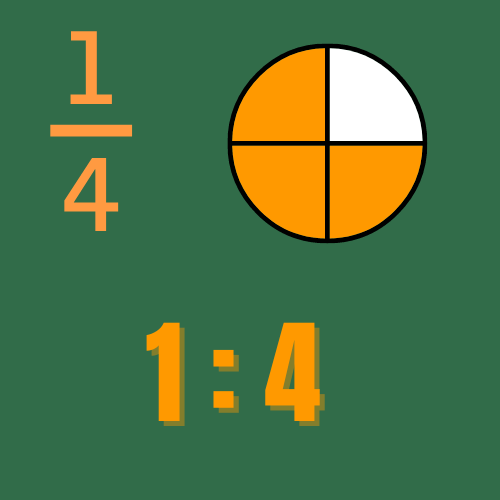
Brüche addieren und subtrahieren bei gleichem Nenner
Die einfachste Art, Brüche zu addieren und zu subtrahieren, tritt auf, wenn sie denselben Nenner haben. Brüche addieren und subtrahieren. In diesem Fall bleibst du einfach beim gemeinsamen Nenner und fügst oder subtrahierst die Zähler.
Ein Bruch mit Zähler gleich Nenner drückt aus, dass du die gesamte Einheit oder Menge besitzt oder verwendest, und er wird oft als “ganze Zahl” oder “Eins” bezeichnet. Es ist eine einfache Möglichkeit zu sagen, dass nichts fehlt oder übrig ist, du hast alles.
In vielen praktischen Anwendungen und mathematischen Berechnungen kann ein Bruch mit Zähler gleich Nenner weiter vereinfacht werden, indem er durch die Zahl 1 ersetzt wird. Dies vereinfacht Berechnungen und macht sie oft übersichtlicher.
Beispiel 1: Brüche mit dem gleichen Nenner addieren
Angenommen, du hast 1/3 eines Kuchens und möchtest 2/3 mehr davon haben. Das bedeutet, du fügst einfach die Zähler zusammen: 1/3 + 2/3 = 3/3. Jetzt hast du den ganzen Kuchen, weil der Zähler gleich dem Nenner ist.
Beispiel 2: Brüche mit dem gleichen Nenner subtrahieren
Nehmen wir an, du hast 5/8 deines Taschengeldes ausgegeben und möchtest wissen, wie viel dir noch bleibt. Du ziehst einfach den ausgegebenen Bruch von 1 ab: 1 – 5/8 = 3/8. Jetzt weißt du, dass dir noch 3/8 deines Taschengeldes übrig sind.
Brüche mit unterschiedlichen Nennern addieren und subtrahieren
Wenn Brüche unterschiedliche Nenner haben, musst du sie zuerst auf den gleichen Nenner bringen, bevor du sie addieren oder subtrahieren kannst. Dies erfordert ein wenig mehr Arbeit, ist aber durchaus machbar.
-
Grundschul-Coach (E-Book)13,99 €inkl. MwSt.
-
Einmaleins Fidget Spinner3,90 €inkl. MwSt.
-
Großer Lerntyp-Test + Lerntipps9,90 €inkl. MwSt.
Schritt 1: Finde einen gemeinsamen Nenner
Um Brüche mit unterschiedlichen Nennern zu addieren oder subtrahieren, musst du zuerst einen gemeinsamen Nenner finden. Der gemeinsame Nenner ist einfach das kleinste Vielfache der beiden Nenner.
Beispiel 3: Brüche mit unterschiedlichen Nennern addieren
Angenommen, du möchtest 1/4 und 1/6 addieren. Der kleinste gemeinsame Nenner ist hier 12, da 12 durch 4 und 6 teilbar sind.
Schritt 2: Ändere die Brüche so, dass sie denselben Nenner haben
Um 1/4 auf den Nenner 12 zu bringen, multiplizierst du sowohl den Zähler als auch den Nenner mit 3. Das ergibt 3/12. Um 1/6 auf den Nenner 12 zu bringen, multiplizierst du sowohl den Zähler als auch den Nenner mit 2. Das ergibt 2/12.
Schritt 3: Addiere die Brüche
Jetzt, da beide Brüche denselben Nenner haben, kannst du die Zähler addieren: 3/12 + 2/12 = 5/12. Das ist das Ergebnis der Addition von 1/4 und 1/6.
Beispiel 4: Brüche mit unterschiedlichen Nennern subtrahieren
Wenn du 5/8 von 3/4 subtrahieren möchtest, findest du zuerst den gemeinsamen Nenner, der hier 8 ist. Dann änderst du 3/4 so, dass es denselben Nenner hat wie 5/8, was ebenfalls 8 ist. Das ergibt 6/8.
Jetzt kannst du die Brüche subtrahieren: 5/8 – 6/8 = -1/8. Das bedeutet, nachdem du 5/8 von 3/4 subtrahiert hast, bleibt dir noch -1/8 übrig, was bedeutet, dass du 1/8 mehr ausgegeben hast, als du hattest.
Häufige Fehler beim Bruchrechnen
Beim Bruchrechnen können einige Fehler auftreten. Hier sind die häufigsten Fehler und wie du sie vermeiden kannst:
- Vergessen des gemeinsamen Nenners: Der wichtigste Schritt beim Addieren oder Subtrahieren von Brüchen mit unterschiedlichen Nennern ist das Finden eines gemeinsamen Nenners. Vergiss nicht, diesen Schritt zu durchlaufen, sonst wird dein Ergebnis nicht korrekt sein.
- Unvollständige Brüche: Stelle sicher, dass deine Brüche vollständig gekürzt sind. Manchmal vergessen Leute, Brüche zu kürzen, und erhalten dadurch falsche Ergebnisse.
- Fehler beim Kürzen: Wenn du Brüche kürzt, achte darauf, dass du sowohl den Zähler als auch den Nenner durch denselben Wert teilst. Ein häufiger Fehler ist es, nur den Nenner zu teilen.
- Vorzeichenfehler: Brüche können negative Vorzeichen haben. Achte darauf, Vorzeichen korrekt zu behandeln, wenn du Brüche addierst oder subtrahierst.
- Fehlende Überprüfung: Vergiss nicht, deine Ergebnisse zu überprüfen, indem du die Brüche auf ihren kleinsten gemeinsamen Nenner reduzierst und sicherstellst, dass sie korrekt gekürzt sind. Überprüfe auch, ob deine Ergebnisse sinnvoll sind. Zum Beispiel kann das Ergebnis einer Addition von Brüchen nicht größer sein als 1, wenn die ursprünglichen Brüche kleiner als 1 sind.
- Verwechslung von Zähler und Nenner: Manchmal können Menschen den Zähler und den Nenner verwechseln, insbesondere wenn sie unter Zeitdruck stehen. Stelle sicher, dass du genau weißt, welcher Teil des Bruchs der Zähler und welcher der Nenner ist.
- Fehlendes Verständnis für den Bruch als Teil: Denke daran, dass ein Bruch einen Teil von etwas darstellt. Ein Bruch wie 3/4 bedeutet, dass du von einer ganzen Einheit 3 von 4 gleich großen Teilen hast. Verstehe dieses Konzept, um Brüche richtig zu verwenden.
- Mangelnde Übung: Bruchrechnen erfordert Übung. Wenn du nicht regelmäßig damit arbeitest, wirst du Schwierigkeiten haben, Fehler zu vermeiden. Übe das Bruchrechnen, um sicherer im Umgang damit zu werden.
Noch mal in Kürze
Bruchrechnen im Alltag ist eine nützliche Fähigkeit, die dir in vielen Situationen helfen kann. Das Hinzufügen und Subtrahieren von Brüchen mag zunächst kompliziert erscheinen, aber mit den richtigen Schritten und etwas Übung kannst du leicht genauere Ergebnisse erzielen. Denke daran, die häufigsten Fehler zu vermeiden, indem du die Grundlagen verstehst, den gemeinsamen Nenner findest und sorgfältig die Brüche addierst oder subtrahierst. Mit ein wenig Übung wirst du bald zum Bruchrechenprofi!
