Einführung in Bruchrechnen: So unterstützt du dein Kind optimal

Bruchrechnen mag auf den ersten Blick einschüchternd wirken, aber keine Sorge, ich werde dir in dieser Einführung in Bruchrechnen zeigen, dass es gar nicht so schwer ist. In diesem Blogartikel werden wir uns Schritt für Schritt dem Bruchrechnen nähern, damit du bald selbstbewusst und sicher mit deinem Kind lernen kannst. Falls du weitere Fragen hast, schau dir unsere Lernvideos zum Thema “Bruchrechnen” an und erkläre dann deinem Kind, wie es funktioniert.

Einführung in Bruchrechnen: Was sind Brüche überhaupt?

Bevor wir in die Tiefe gehen, lassen uns zuerst verstehen, was Brüche überhaupt sind. Ein Bruch besteht aus zwei Teilen: dem Zähler (oben) und dem Nenner (unten). Der Zähler zeigt uns, wie viele Teile wir von etwas haben, während der Nenner angibt, in wie viele gleich große Teile wir die Gesamtheit aufteilen. Der Bruchstrich ist dabei genau das Gleiche wie ein Geteilt-Zeichen.

Beispiel 1: Der einfache Bruch

Schauen wir uns einen einfachen Bruch an, zum Beispiel 1/4. Hier ist 1 der Zähler, was bedeutet, dass wir einen Teil von etwas haben, und der Nenner 4 zeigt uns, dass wir die Gesamtheit in vier gleich große Teile aufteilen. 1/4 ist also einer von 4 Teilen. 4/4 wären also so viel wie 1 Ganzes, denn es handelt sich um vier von vier Teilen.

Beispiel 2: Ein gemischter Bruch

Manchmal begegnen wir auch sogenannten gemischten Brüchen. Diese setzen sich aus einem ganzzahligen Teil und einem Bruchteil zusammen. Zum Beispiel 2 1/3. Hier ist 2 der ganze Teil, und 1/3 ist der Bruchteil, der uns sagt, dass wir noch ein Drittel von etwas haben. Du hast also bei 5 3/5 fünf ganze Teile, beispielsweise Apfelsinen und noch einen Teil einer 6. Apfelsine, nämlich 3/5.

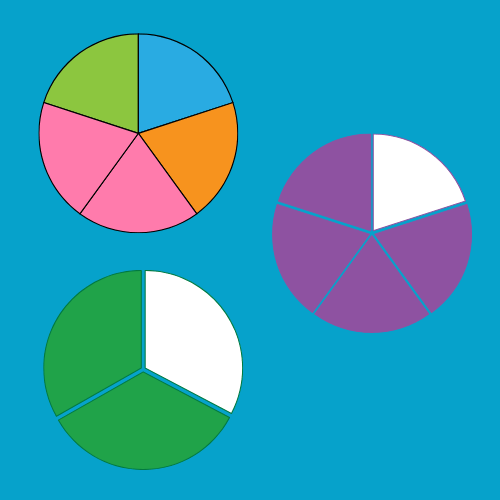
Jetzt, wo wir wissen, was Brüche sind, können wir uns den Grundrechenarten widmen: Addition, Subtraktion, Multiplikation und Division.

Grundrechenarten mit Brüchen: Addition und Subtraktion

Beim Addieren oder Subtrahieren von Brüchen müssen die Nenner gleich sein. Wenn sie es nicht sind, müssen wir sie zuerst auf denselben Nenner bringen. Wir machen das, indem wir beide Brüche so umformen, dass sie denselben Nenner haben.

Beispiel 3: Addition von Brüchen

Angenommen, wir möchten 1/4 + 1/6 addieren. Die Nenner sind unterschiedlich, also müssen wir sie gleich machen. Wir können den kleinsten gemeinsamen Nenner verwenden, der hier 12 ist. Das ergibt:

1/4 + 1/6 = (3/3)(1/4) + (2/2)(1/6) = 3/12 + 2/12 = 5/12

Also ist 1/4 + 1/6 = 5/12.

Beispiel 4: Subtraktion von Brüchen

Die Subtraktion von Brüchen funktioniert genauso wie die Addition. Wir müssen zuerst die Nenner gleich machen und dann die Zähler subtrahieren.

Grundrechenarten mit Brüchen: Multiplikation und Division

Die Multiplikation von Brüchen ist relativ einfach. Du multiplizierst einfach die Zähler miteinander und die Nenner miteinander.

Beispiel 5: Multiplikation von Brüchen

Wenn wir 1/2 * 2/3 multiplizieren, ergibt das:

1/2 * 2/3 = (12)/(23) = 2/6

Aber wir können Brüche oft kürzen, um sie einfacher zu machen. In diesem Fall können wir sowohl den Zähler als auch den Nenner durch 2 teilen:

2/6 = (2/2) * (1/3) = 1/3

Jetzt haben wir 1/3.

Die Division von Brüchen ist ein bisschen komplizierter. Statt zu teilen, drehen wir den zweiten Bruch um und multiplizieren ihn mit dem ersten.

Beispiel 6: Division von Brüchen

Wenn wir 1/2 ÷ 3/4 teilen, wird es zu:

1/2 * 4/3 = (14)/(23) = 4/6

Und wie zuvor können wir diesen Bruch kürzen:

4/6 = (4/2) * (1/3) = 2/3

Jetzt haben wir 2/3.

Brüche in Dezimalzahlen umwandeln

Manchmal ist es praktisch, Brüche in Dezimalzahlen umzuwandeln, besonders wenn du mit Geldbeträgen oder Messungen arbeitest. Dazu teilen wir den Zähler durch den Nenner. Du erinnerst dich? Der Bruchstrich ist wie ein Geteilt -Zeichen.

Beispiel 7: Umwandlung in Dezimalzahlen

Um 3/4 in eine Dezimalzahl umzuwandeln, dividieren wir 3 durch 4:

3/4 = 3 ÷ 4 = 0,75

Also entspricht 3/4 der Dezimalzahl 0,75.

Grundrechenarten mit Brüchen: Prozentrechnung und Brüche

Brüche sind eng mit Prozenten verbunden. Ein Bruch kann leicht in eine Prozentzahl umgewandelt werden, indem man ihn in einen Hundertstel-Bruch umwandelt.

Beispiel 8: Umwandlung in Prozent

Angenommen, wir haben den Bruch 2/5 und möchten ihn in eine Prozentzahl umwandeln. Zuerst wandeln wir ihn in einen Hundertstel-Bruch um:

2/5 = (2/5) * (20/20) = 40/100

Jetzt sehen wir, dass 2/5 40 Hundertstel oder 40% entsprechen.

Praktische Anwendungen von Bruchrechnung

Jetzt fragst du dich vielleicht, warum du überhaupt Bruchrechnung lernen solltest. Nun, Brüche sind in vielen Aspekten des täglichen Lebens nützlich. Hier haben wir einige Beispiele für dich zusammengestellt, die dir bestimmt bekannt vorkommen.

• Kochen und Backen

Wenn du gerne kochst oder bäckst, wirst du oft mit Bruchzahlen in Rezepten konfrontiert. Zum Beispiel könnte ein Kuchenrezept verlangen, dass du 3/4 Tassen Zucker hinzufügst. Wenn du Bruchrechnung verstehst, kannst du solche Rezepte leichter umsetzen.

• Geld und Finanzen

Brüche sind auch im Finanzbereich wichtig. Wenn du herausfinden möchtest, wie viel Rabatt du auf einen Artikel bekommst oder wie viel Steuern du bezahlen musst, kannst du Bruchrechnung verwenden.

• Konstruktion und Handwerk

Wenn du handwerklich begabt bist oder Bauprojekte durchführst, wirst du Brüche verwenden, um Maße und Abmessungen zu berechnen. Zum Beispiel könntest du Holz in Stücke schneiden müssen, die 3/8 Zoll dick sind.

• Medizin und Gesundheit

Auch im medizinischen Bereich sind Brüche wichtig. Wenn ein Arzt dir eine Medikamentendosis verschreibt, könnte sie in Bruchteilen einer Tablette gemessen werden. Es ist wichtig zu wissen, wie man diese Brüche korrekt berechnet.

• Einkaufen

Wenn du im Supermarkt einkaufst und Artikel im Angebot sind, möchtest du vielleicht wissen, wie viel du sparst. Das erfordert das Verständnis von Bruchrechnung, um den Rabatt korrekt zu berechnen.

• Zeitmanagement

Wenn du deinen Tag planst und Aufgaben in Zeitblöcke aufteilst, könntest du Brüche verwenden, um sicherzustellen, dass du genügend Zeit für jede Aufgabe hast.

• Reisen

Wenn du eine Reise planst und die Entfernung in Bruchteilen der Gesamtstrecke berechnen möchtest, wird das Verständnis von Bruchrechnung hilfreich sein.

Tipps zum Üben

Um besser im Umgang mit Brüchen zu werden, hier einige Tipps:

1. Übe regelmäßig: Wie bei jeder mathematischen Fähigkeit gilt auch hier, dass Übung den Meister macht. Löse regelmäßig Bruchrechenübungen, um deine Fertigkeiten zu verbessern.
2. Verstehe die Grundlagen: Stelle sicher, dass du die Grundlagen der Bruchrechnung verinnerlicht hast, bevor du zu komplexeren Aufgaben übergehst.
3. Nutze Online-Ressourcen: Das Internet bietet viele kostenlose Ressourcen, darunter Übungsaufgaben, Video-Tutorials und interaktive Bruchrechner.
4. Frage nach Hilfe: Wenn du Schwierigkeiten hast, zögere nicht, um Hilfe zu bitten. Ein Lehrer, Tutor oder Mitschüler kann dir bei Fragen oder Problemen helfen.
5. Verwende Bruchrechnung im Alltag: Versuche, Bruchrechnung in alltäglichen Situationen anzuwenden, um deine Fertigkeiten zu festigen.

Kurze Zusammenfassung der Einführung in Bruchrechnen

Bruchrechnung mag anfangs verwirrend erscheinen, aber sie ist eine äußerst nützliche Fertigkeit im täglichen Leben. Mit den Grundlagen, die du in diesem Artikel gelernt hast, bist du auf dem besten Weg, Brüche zu verstehen und erfolgreich anzuwenden. Übung und Geduld sind der Schlüssel, um deine Fertigkeiten zu verbessern. Also keine Angst vor den Brüchen – du kannst sie meistern und sie werden dir in vielen Lebenssituationen nützlich sein. Diese Einführung in Bruchrechnen ist dir dabei eine erste Hilfe.